pTFCE

Logo

by Tamas Spisak

View the Project on GitHub spisakt/pTFCE

Probabilistic Threshold-free Cluster Enhancement

Welcome to the wiki pages of pTFCE, developed and maintained by the Predictive Neuroimagiong Laboratory (PNI-lab) of the University Hospital Essen, Germany.

News

New R-package release 0.2.2, with a small bugfix (fixing NaN values at low Z-scores on imgages with low-smoothness).

From 01.01.2020, the maintanence and developement of pTFCE will be continued in the recently established Predictive Neuroimagiong Laboratory (PNI-lab), lead by Tamas Spisak.

Check out this thread on applying pTFCE on both side of your Z-score map.

v0.2.0 available for both the R-package and the SPM Toolbox. It features a speed performance patch: pTFCE is now almost twice as fast!

Since the start, 700 unique visitors, >1000 visits and a lot of e-mails. Thanks for all your interest!

Smoothness estimation is now possible based on 4D residual data

pTFCE (probabilistic TFCE) is a cluster-enahncement method to improve detectability of neuroimaging signal. It performs topology-based belief boosting by integrating cluster information into voxel-wise statistical inference.

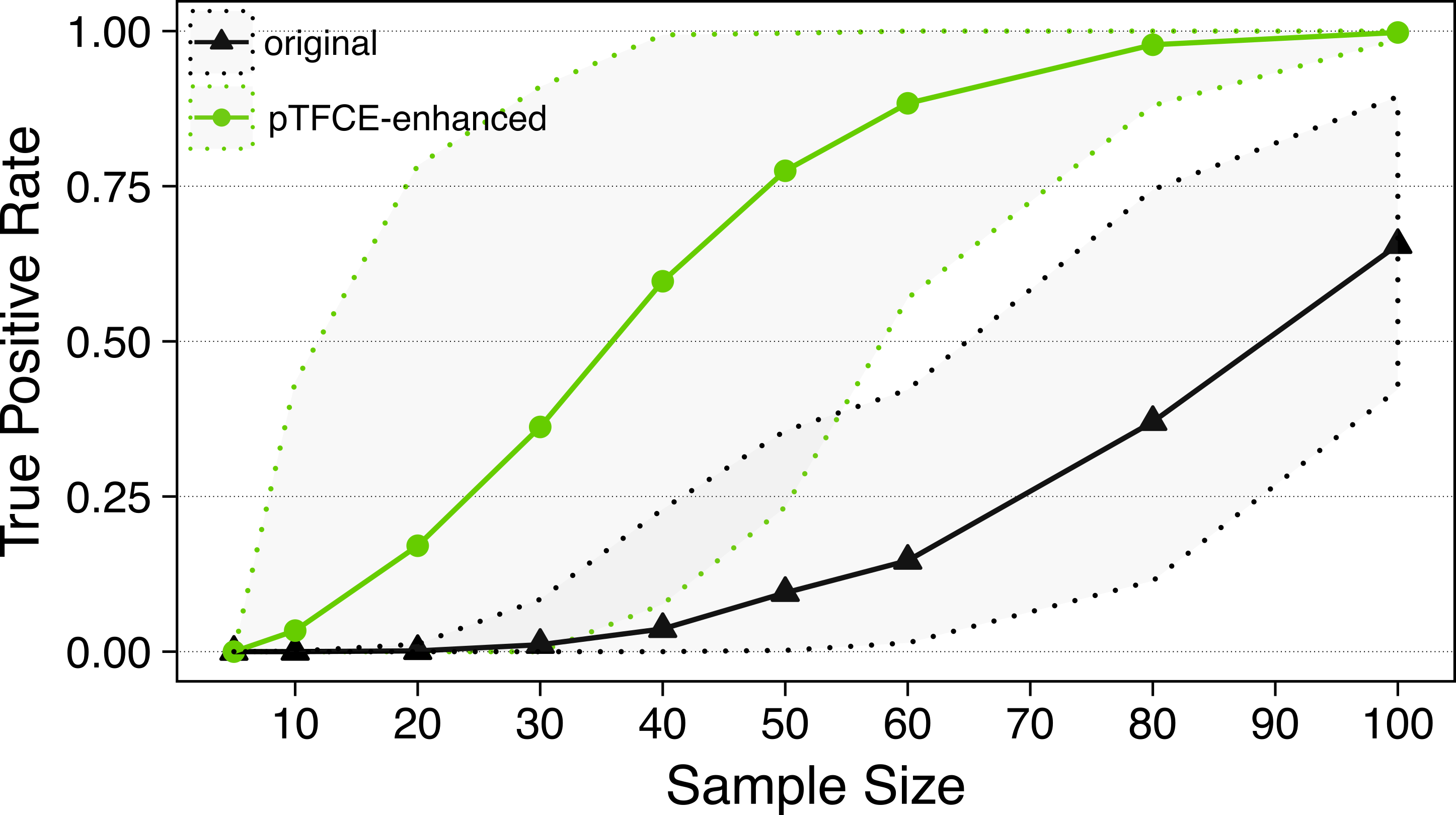image Figure 1. pTFCE achieves a significant increase in statistical power in most of the typical fMRI processing scenarios. See the paper for details.

For a detailed description and theory, please refer to (and please cite):

Tamás Spisák, Zsófia Spisák, Matthias Zunhammer, Ulrike Bingel, Stephen Smith, Thomas Nichols, Tamás Kincses, Probabilistic TFCE: a generalised combination of cluster size and voxel intensity to increase statistical power. Neuroimage, 185:12-26.

DOI:10.1016/j.neuroimage.2018.09.078

Download Open Source Love svg1

R-package & Installation Maintenance CircleCI GitHub license GitHub release GitHub issues GitHub issues-closed

SPM Matlab Toolbox & Installation
Maintenance GitHub license GitHub release GitHub issues GitHub issues-closed

Users’ Guide Contents

  1. Overview
  2. Relation to TFCE
  3. The R-package
    3.1 Installation
    3.2 Usage
  4. The SPM Toolbox
    4.1 Installation
    4.2 Usage
  5. The FSL extension
    5.1 Installation
    5.2 Usage
  6. The Nipype interface
    Citation and References

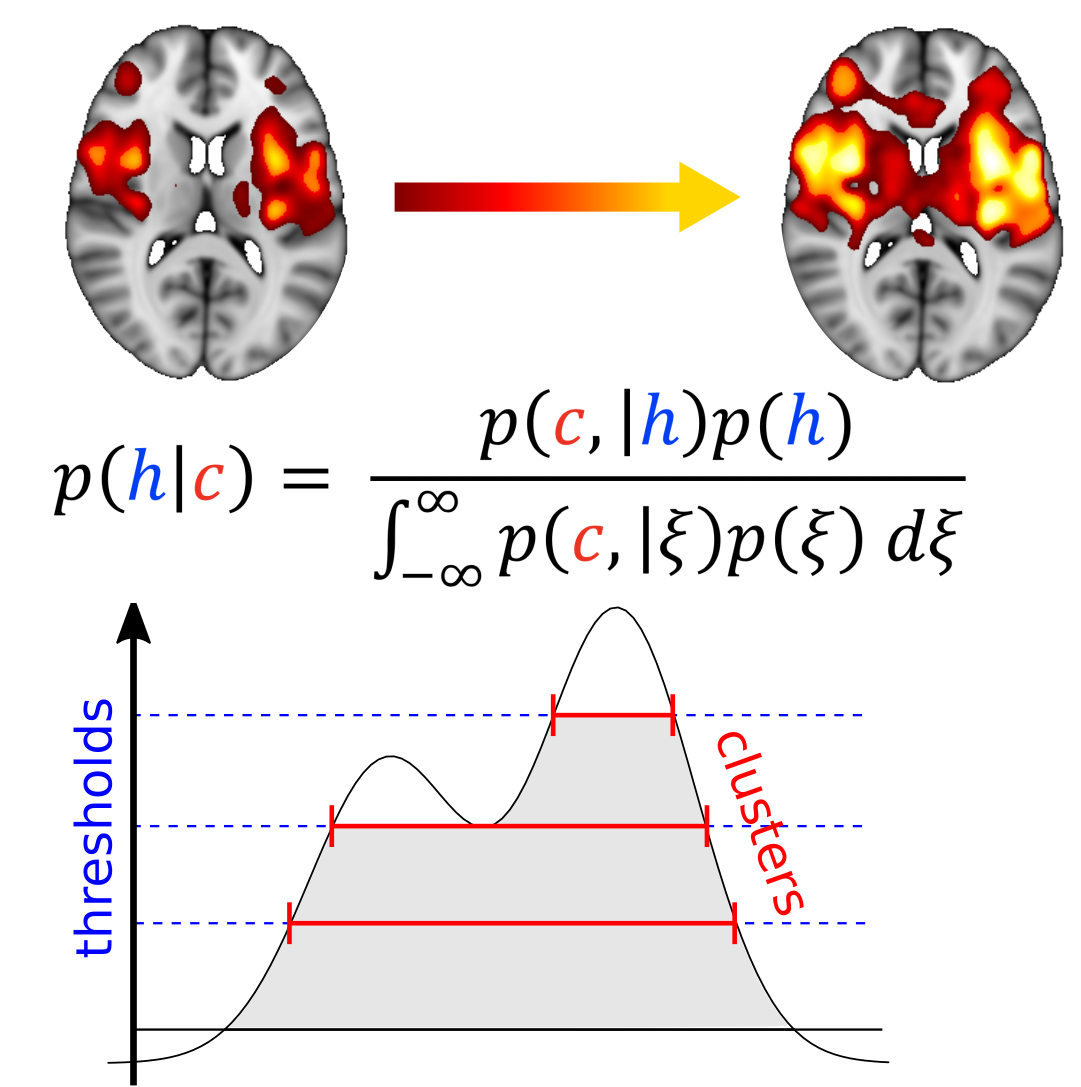
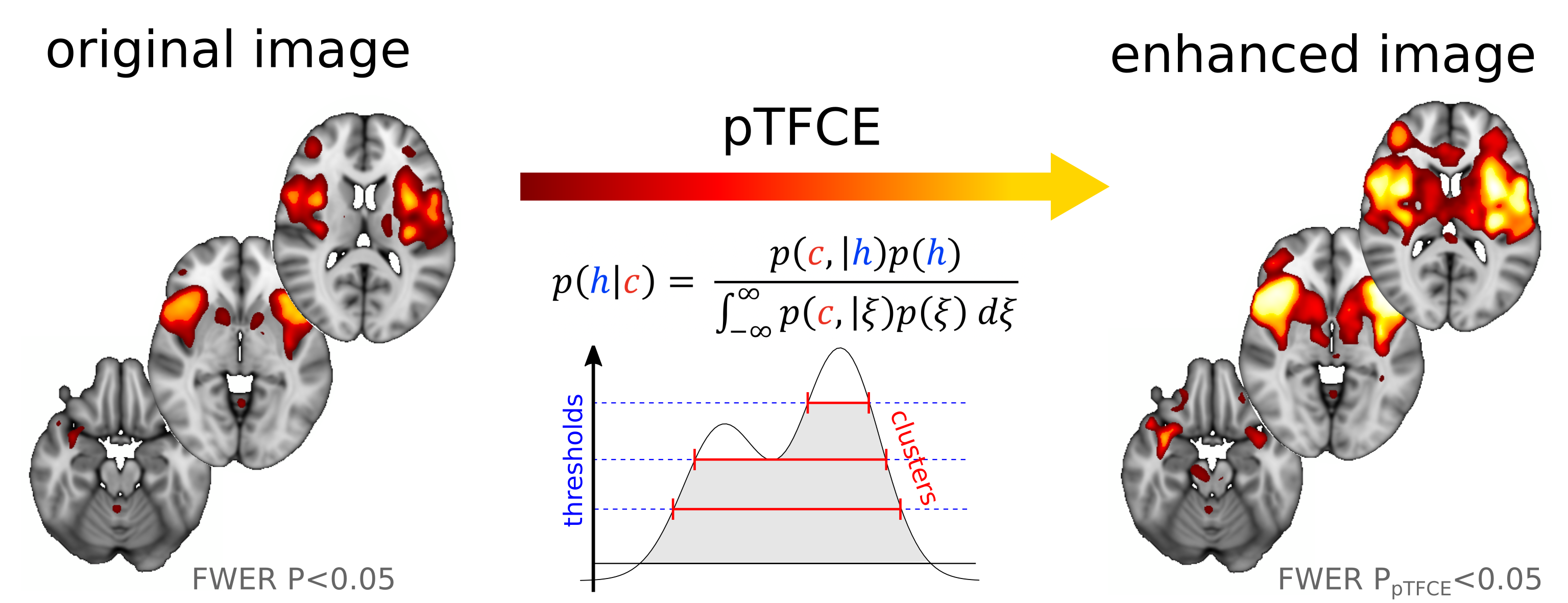image Figure 2. A graphical representation of pTFCE depicting the integaration of cluster probabilities at various cluster-forming threshold via Bayes’ Theorem and our incremental probability aggregation technique.